Majorana fermions have been theoretically predicted more than 70 years ago, but whether they exist as fundamental particles remains an open question to this day. The prediction and subsequent experimental indications of Majorana bound states as quasiparticles in certain solid-state systems have therefore sparked a flurry of research activity, driven also by their usefulness in topological quantum computing.

Parafermionic bound states are generalizations of MBS which occur in strongly correlated systems, such as fractional quantum Hall states. They are more suitable for topological quantum computation than MBS because their braiding allows additional protected operations. We explore ways to experimentally realize such parafermionic states and how to use them for quantum computation. An essential prerequisite is to better understand the interplay between two important “macroscopic” quantum effects: superconductivity and quantum Hall physics.

References:

1. Michelsen, Andreas Bock and Recher, Patrik and Braunecker, Bernd and Schmidt, Thomas L., Supercurrent-Enabled Andreev Reflection in a Chiral Quantum Hall Edge State, Physical Review Research 5, 013066 (2023)
2. Teixeira, Raphael L. R. C. and Haller, Andreas and Singh, Roshni and Mathew, Amal and Idrisov, Edvin G. and Dias da Silva, Luis G. G. V. and Schmidt, Thomas L., Overlap of Parafermionic Zero Modes at a Finite Distance, Physical Review Research 4, 043094 (2022)
3. Michelsen, Andreas B. and Schmidt, Thomas L. and Idrisov, Edvin G., Current Correlations of Cooper-Pair Tunneling into a Quantum Hall System, Phys. Rev. B 102, 125402 (2020)
4. Schmidt, Thomas L., Bosonization for Fermions and Parafermions, Eur. Phys. J. Special Topics 229, 621 (2020)
5. Groenendijk, Solofo and Calzona, Alessio and Tschirhart, Hugo and Idrisov, Edvin G. and Schmidt, Thomas L., Parafermion braiding in fractional quantum Hall edge states with a finite chemical potential, Phys. Rev. B 100, 205424 (2019)
6. Alessio Calzona and Tobias Meng and Maura Sassetti and Thomas L. Schmidt, Z4 parafermions in one-dimensional fermionic lattices, Phys. Rev. B 98, 201110(R) (2018)
7. Christopher J. Pedder and Tobias Meng and Rakesh Tiwari and Thomas L. Schmidt, Missing Shapiro steps and the $8π$-periodic Josephson effect in interacting helical electron systems, Phys. Rev. B 96, 165429 (2017)

Skyrmions are topological magnetization patterns, which have been studied intensively over the past decade because of their suitability of information storage in magnetic memory chips. They have been mostly described by classical magnetism, but nanoscale skyrmions discovered in recent years raise the question about their quantum mechanical properties. An important cause of skyrmion formation is the Dzyaloshinskii-Moriya interaction, which exists is crytals with broken inversion symmetry.

We investigate Heisenberg-like quantum systems with Dzyaloshinskii-Moriya interactions in one- and two-dimensional quantum magnets, described by Heisenberg-like Hamiltonians. We use a combination of analytical techniques (bosonization, spin-wave theory, mean-field theory) and numerical techniques (exact diagonalization, density-matrix renormalization group).

References:

1. Haller, Andreas and Díaz, Sebastián A. and Belzig, Wolfgang and Schmidt, Thomas L., Quantum Magnetic Skyrmion Operator, Physical Review Letters 133, 216702 (2024)
2. Haller, Andreas and Groenendijk, Solofo and Habibi, Alireza and Michels, Andreas and Schmidt, Thomas L., Quantum Skyrmion Lattices in Heisenberg Ferromagnets, Physical Review Research 4, 043113 (2022)
3. Tschirhart, Hugo and Ong, Ernest T. S. and Sengupta, Pinaki and Schmidt, Thomas L., Phase diagram of spin-1 chains with Dzyaloshinskii-Moriya interaction, Phys. Rev. B 100, 195111 (2019)

Funding:

1. FNR CORE “Detecting Quantum Skyrmions” (DeQuSky).
2. FNR AFR “Spin-orbit coupling in low-dimensional correlated materials” (SOCMAT).

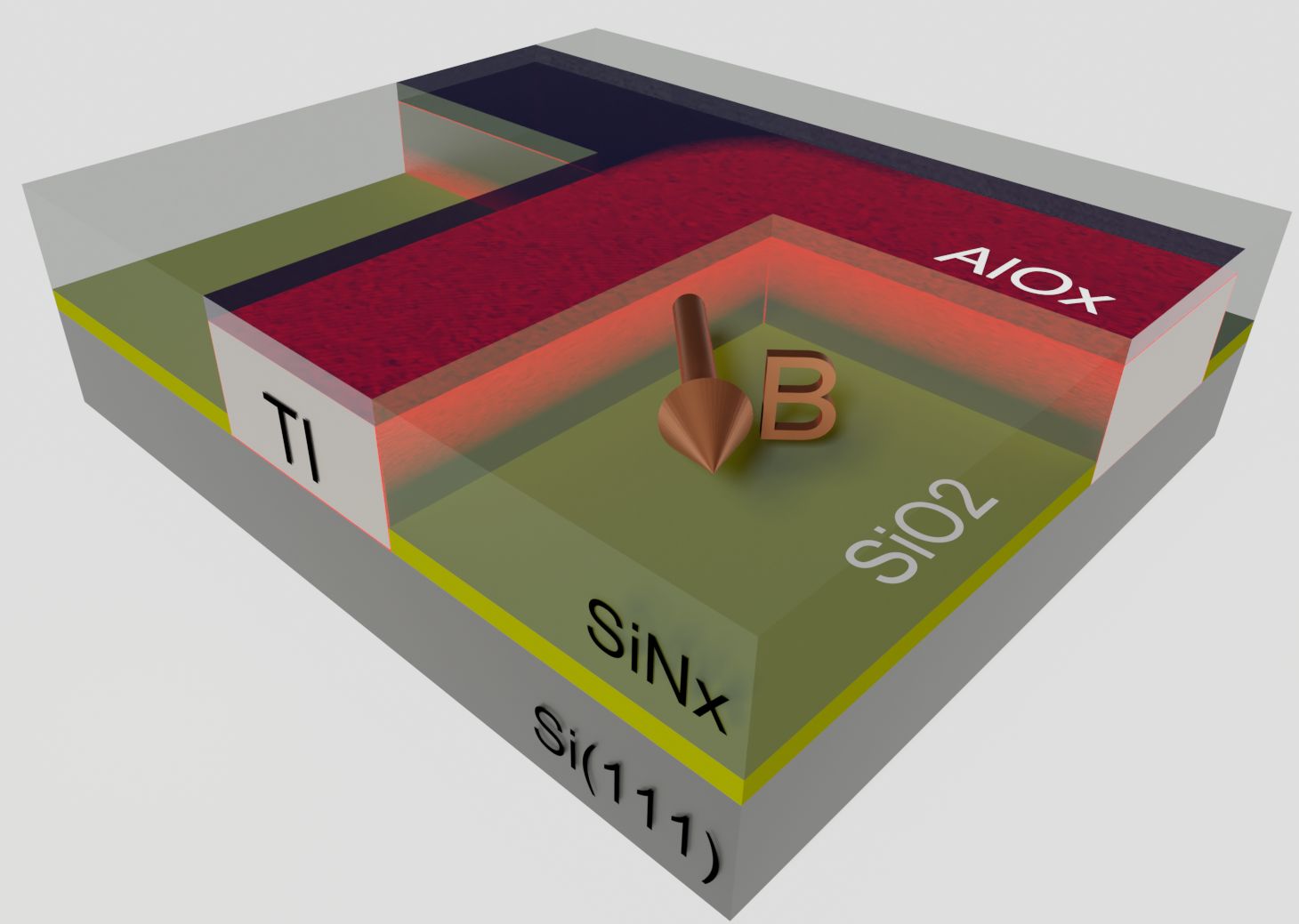Topological materials have electronic band structures which can be characterized by a topological, quantized winding number. A prominent example are topological insulators, which behave like band insulators in the bulk but have gapless, metallic states on their surfaces. Most topological materials have spin-orbit coupling, so the orbital motion of electrons is strongly correlated with their spin. This gives rise to interesting spin and charge transport properties in these materials.

We investigate electronic and optical properties of topological materials. In recent year, we have studied in particular, open topological quantum systems which are coupled to an environment, as well as the realization of general-relativistic effects in topological systems. Currently, we are also studying magnetic topological insulators and their interplay with superconductors.

References:

2. Habibi, Alireza and Musthofa, Ahmad Z. and Adibi, Elaheh and Ekström, Johan and Schmidt, Thomas L. and Hasdeo, Eddwi H., Kerr and Faraday Rotations in Topological Flat and Dispersive Band Structures, New Journal of Physics 24, 063003 (2022)
3. De Beule, Christophe and Groenendijk, Solofo and Meng, Tobias and Schmidt, Thomas L., Artificial Event Horizons in Weyl Semimetal Heterostructures and Their Non-Equilibrium Signatures, SciPost Phys. 11, 095 (2021)
4. Farias, M. Belén and Groenendijk, Solofo and Schmidt, Thomas L., Generalized Chern Numbers Based on Open System Green’s Functions, New Journal of Physics 23, 073009 (2021)
5. Kölzer, Jonas and Moors, Kristof and Jalil, Abdur Rehman and Zimmermann, Erik and Rosenbach, Daniel and Kibkalo, Lidia and Schüffelgen, Peter and Mussler, Gregor and Grützmacher, Detlev and Schmidt, Thomas L. and Lüth, Hans and Schäpers, Thomas, In-Plane Magnetic Field-Driven Symmetry Breaking in Topological Insulator-Based Three-Terminal Junctions, Commun. Mater. 2, 116 (2021)

Funding:

1. QuantERA “Magnetic topological insulators for robust Majorana bound states” (MAGMA)
2. FNR CORE “Detecting Quantum Skyrmions” (DeQuSky).